
| 授業場所 |
 |
□普通教室 □コンピュータ教室 ■特別教室 □体育館
□運動場 □屋外 □その他〔 〕 |
 |
 |
 |
| 授業形態 |
 |
■一斉学習 □グループ学習 □個別学習 □補習 □その他〔 〕 |
 |
 |
 |
| ITを活用する場面 |
 |
■導入 ■展開 □まとめ □その他〔 〕 |
 |
 |
 |
| ITを主に活用する者 |
 |
■教員 ■学習者 □その他〔 〕 |
 |
 |
 |
| ITを活用する目的 |
 |
□課題の提示 □動機付け □教員の説明資料 □学習者の説明資料 □繰り返しによる定着 ■モデルの提示 □失敗例の提示 □体験の想起 □比較 □振り返り ■体験の代行 □その他〔 〕 |
 |
 |
 |
| 活用するIT |
 |
■コンピュータ ■プロジェクタ ■スクリーン □電子ホワイトボード □実物投影機 □デジタルカメラ □ビデオ □インターネット □デジタルコンテンツ □CD-ROM □スピーカー □その他〔 〕 |
|


実際に生徒が作成したものを紹介して,いろんなケースを考える機会を与える。


「二項定理とパスカルの三角形」
学習指導要領との対応:
内容 (3) 場合の数と確率 ア 順列・組合せ


| (1) |
二項係数の性質を定着させるとともに,数学的現象を一歩深めて分析することのおもしろさを感じさせる。 |


| (1) |
数学Iで学習した「式の展開」を復習する。
| (ア) |
(a+b)2 = 1 a2+
2 ab+ 1 b2 |
| (イ) |
(a+b)3 = 1 a3+
3 a2b+ 3 ab2+ 1 b3 について,次のように考える。 |
|
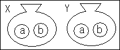
| (ア)の解説:X,Yの袋には,それぞれaとbの2個のボールが入っていて,それぞれの袋からいずれかのボールを1個ずつ取り出す場合の数は,次の4通りが考えられる。 |
 |
 |
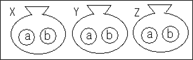
| (イ)の解説:X,Y,Zの袋には,それぞれaとbの2個のボールが入っていて,それぞれの袋からいずれかのボールを1個ずつ取り出す場合の数は,次の8通りが考えられる。 |
 |
 |
|
| (2) |
二項係数が「組合せ(Combination)」で求められることを学習する。
| 同じように,W,X,Y,Zの袋に,それぞれaとbの2個のボールが入っていて,それぞれの袋からいずれかのボールを1個ずつ取り出す場合の数は,何通りあるか。 |
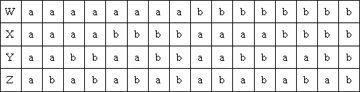 |
答えは,上記の16通りで,このとき,次のことが言える。
aaaaは,1 通り。すなわち,4つから0個のbを選ぶ組合せ:4C0 =
1
aaabは,4 通り。すなわち,4つから1つのbを選ぶ組合せ:4C1 =
4
aabbは,6 通り。すなわち,4つから2つのbを選ぶ組合せ:4C2 =
6
abbbは,4 通り。すなわち,4つから3つのbを選ぶ組合せ:4C3 =
4
bbbbは,1 通り。すなわち,4つから4つのbを選ぶ組合せ:4C4 =
1 |
|
|
|
| (3) |
パスカルの三角形の性質を見つける。

| (a+b)n の展開式の各項の係数だけを列挙すると次のようになる。 |
| (a+b)2 の場合: |
|
|
|
1 |
|
2 |
|
1 |
|
|
|
|
| (a+b)3 の場合: |
|
|
1 |
|
3 |
|
3 |
|
1 |
|
|
|
| (a+b)4 の場合: |
|
1 |
|
4 |
|
6 |
|
4 |
|
1 |
|
|
| (a+b)5 の場合: |
1 |
|
5 |
|
10 |
|
10 |
|
5 |
|
1 |
|
気づいたことをあげてみよう。たとえば,
(a+b)2 の係数の和:1+2+1= 4=22
(a+b)3 の係数の和:1+3+3+1= 8=23
(a+b)4 の係数の和:1+4+6+4+1= 16=24
(a+b)5 の係数の和:1+5+10+10+5+1=32=25
(a+b)n の係数の和を予想しよう。すなわち,
nC0+nC1+nC2+…+nCn-2+nCn-1
+nCn =[ ? ]
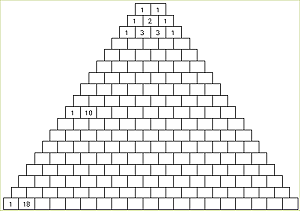
ほかに気づいたことがあればあげてみよう。そして,見つけた法則を使って下の箱を埋めてみよう。 |
|
|
| (4) |
パスカルの三角形の数を色分けすることによって見られるパターンの変化から,数学的分析のおもしろさを感じさせる。

手作業で色分けをしてルールをつかんだ上で,「Mathematica」という数学ソフトを使って,コンピュータ上で「パスカルの三角形」の性質を調べる実験を行う。
あらかじめ用意した「pascal.nb」という教材を使って,二項係数の計算,パスカルの三角形の数列を偶数と奇数で塗り分けるプログラムなどに取り組む。 |
|
|
|
| (5) |
コンピュータを使って瞬時に計算,シミュレーションを行うことで,手作業では不可能なさまざまなパターンを見つけさせる。

| 偶数奇数による色分けだけでなく,設定した数で割り切れるか割り切れないかで色を塗り分けながら,さまざまなパターンの変化を調べ,パスカルの三角形の性質を探る。 |
|
|
|


| (1) |
決まった公式を覚えるという形態をできるだけ避けて,試行錯誤を行う中で自ら発見したり,もっと調べてみたいと思うような気持ちを引き出したいと考えた。
コンピュータを使った視覚的な教材は,興味関心を引き出しやすい。また,必ずしも生徒に作業させなくても,短時間で視覚的教材を提示するだけでも効果があると思われる。 |


| (1) |
パスカルの三角形の色塗りを行うMathematicaプログラム |
| |
1.
|
偶数を白く塗る
pascal[m_] :=Module[{a, b, c},
a = {1/2, -Sqrt[3]/2};
b = {-1/2, -Sqrt[3]/2};
p[n_, k_] := n b + k(a - b);
c = Table[If[EvenQ[Binomial[n, k]],
Circle[p[n, k], 1/2], {RGBColor[0, 0, 1], Disk[p[n, k], 1/2]}],
{n, 0, m}, {k, 0, n}];
Show[Graphics[c, AspectRatio -> Automatic]];]
pascal[40]

|
| |
2. |
設定した数の倍数を白く塗る
pascal2[r_, m_] :=Module[{a, b, c},
a = {1/2, -Sqrt[3]/2};
b = {-1/2, -Sqrt[3]/2};
p[n_, k_] := n b + k(a - b);
c = Table[If[Mod[Binomial[n, k], r] == 0,
Circle[p[n, k], 1/2], {RGBColor[0, 0, 1], Disk[p[n, k], 1/2]}],
{n, 0, m}, {k, 0, n}];
Show[Graphics[c, AspectRatio -> Automatic]];]
pascal2[3, 40] |
|

